ここ数カ月くらい2歳11か月の娘はピアノを習っているのですが、4分音符と2分音符の違いを教えるにあたって「なるほどなあ」と思ったことがありました。
娘は「いち、に、さん、し、」と数字を数えるのは早くからできていて、例えばマンションを1フロアずつ上がると「いっかい、にかい、」となるのは問題なく分かっていたようでした。お友達が大きくなると、「ぜろさい、いっさい、にさい、」と変わるのも分かるようです。
なので、ピアノの幼児教育における「4分音符はリンゴ1個分、2分音符はリンゴ2個分、」という教え方もすぐわかるかなと思ったのですが…、全く分からず。かなり根気よく教えたのですが、けっきょく最後まで理解することなく次のレッスン日を迎えてしまいました。
音の長さを教えるために、ブドウやアメを使っていました。1つなら4分音符、半分なら8分音符、4つなら全音符という具合です。1つなら問題なく分かるのですが、2つの段階でもう分かりません。いくつかのブドウを「いち、に、さん、」と数えるのも、直線状に置いていれば簡単に数えられますが、固めて置くとほとんど数えられません。
娘が繰り返し言っていたのは、「ひとつがたくさん」という表現でした。「このぶどうとこのぶどうはちがう」とも。最終的には「みっつじゃない。ひとつ、ひとつ、ひとつ!」と怒っていました^^;
どうやら娘にとって、数は「前に進む段階のラべリング」であるようでした。
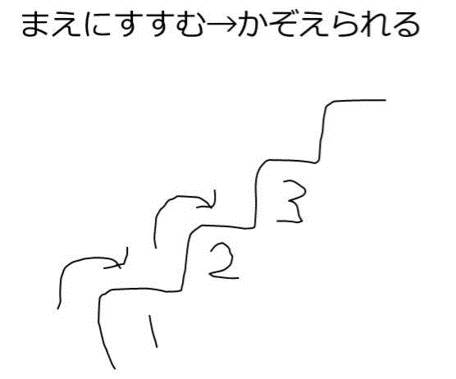
個体の集合をラべリングするには、個体同士の違いが気になってできないみたい。私から見るとブドウは全部同じに見えますが、娘には全然違って見えるのか。
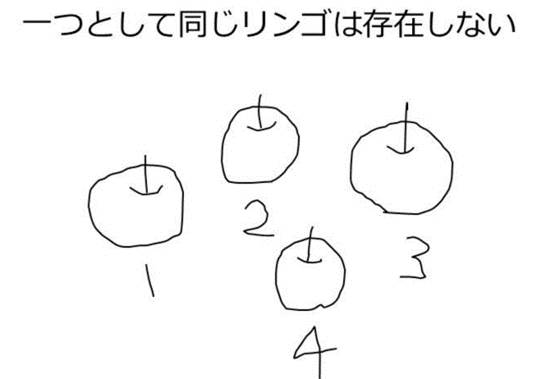
形の違いという話なら、実はもっと難しいのかも。同じ素材・色のブロックでも形が違ったりするし…
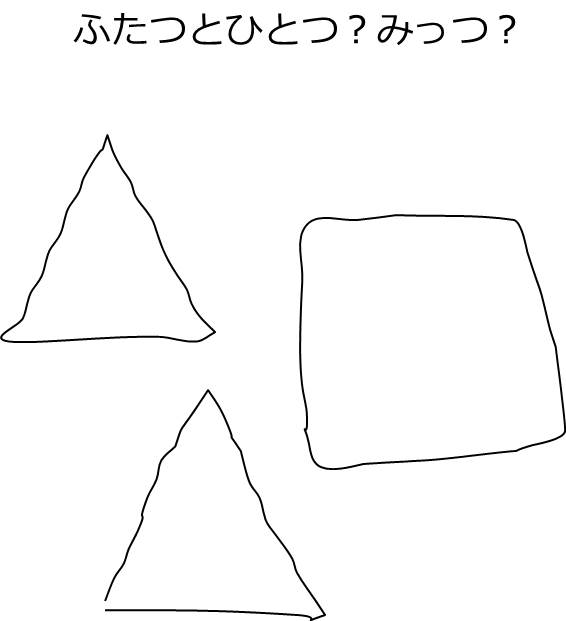
形まで全く同じでも、向きが違ったらどうでしょうか?

そう考えていくと、世の中に全く同じ2つの物は存在しないのだから、「ある固形物のかたまりの個数」を数えるのって難しいことのような気がしてきました。無視して良い差異ってどのくらいの違い?自分にとっては微妙な差異だと思っていたことも、差異を大きくしていくと途端におかしい感じに。

ここまで来るとさすがに大人でも「ひとつがみっつ!」と怒りたくなりますね。
モノとしての固体感が薄れて行ったらどうなんでしょうか?


簡単に形を変えられるものでも、なんとなくかたまり感があると数えられる気がしますね。
以上、とりとめのない話でした。
さて、どうやって2分音符を分かってもらおうかな~^^;



